オームの法則から広がる世界:V = RI
電気回路の基本法則であるオームの法則「V = RI」は、非常にシンプルながらも深い意味を持っています。
ここでの「V」は電圧(ボルト)、「I」は電流(アンペア)、「R」は抵抗(オーム)です。
この式を直感的に理解するには、「電圧は押す力」「電流は流れ」「抵抗は流れにくさ」と捉えるのがポイントです。
たとえば水道管をイメージすると、電圧は水を押すポンプの力、電流は流れる水の量、抵抗は細い管のように水の流れを妨げるものと考えることができます。
この考え方は、実は力学の式「F = bv」──力が速度に比例するような粘性抵抗──とよく似ています。
つまり、**オームの法則は「力 = 抵抗 × 速度」**の電気版なのです。
RLC回路とバネマスダンパ系の比較
オームの法則に加えて、コイル(インダクタ)やコンデンサ(キャパシタ)を回路に加えると、さらに面白い世界が見えてきます。
以下は、電気回路と力学系の典型的な対応関係です。
| 力学系 | 電気回路 |
|---|---|
| 力 F [N] | 電圧 V [V] |
| 質量 m [kg] | インダクタンス L [H] |
| ダンパ係数 c [Ns/m] | 抵抗 R [Ω] |
| バネ定数 k [N/m] | 1/キャパシタンス 1/C  |
| 変位 x [m] | 電荷 q [C] |
| 速度 v = dx/dt [m/s] | 電流 I = dq/dt [A](=[C/s]) |
このように、それぞれの要素が1対1で対応していることがわかります。
また、力学系でいうと、「mx” + bx’ + kx = F」というバネマスダンパ系の微分方程式があります。
これと全く同じ構造の式が、RLC直列回路では「L I” + R I’ + (1/C) I = V」として現れます。
つまり、電流の時間変化を質点の運動とみなすことができるわけです。
その結果、共振や減衰などの振る舞いも、まったく同じ数式で解析できます。
下図に視覚的なイメージを掲載します。電気回路(RLC)と力学系(質量・バネ・ダンパ)には構成要素レベルでの1対1の対応関係があることがわかるかと思います。
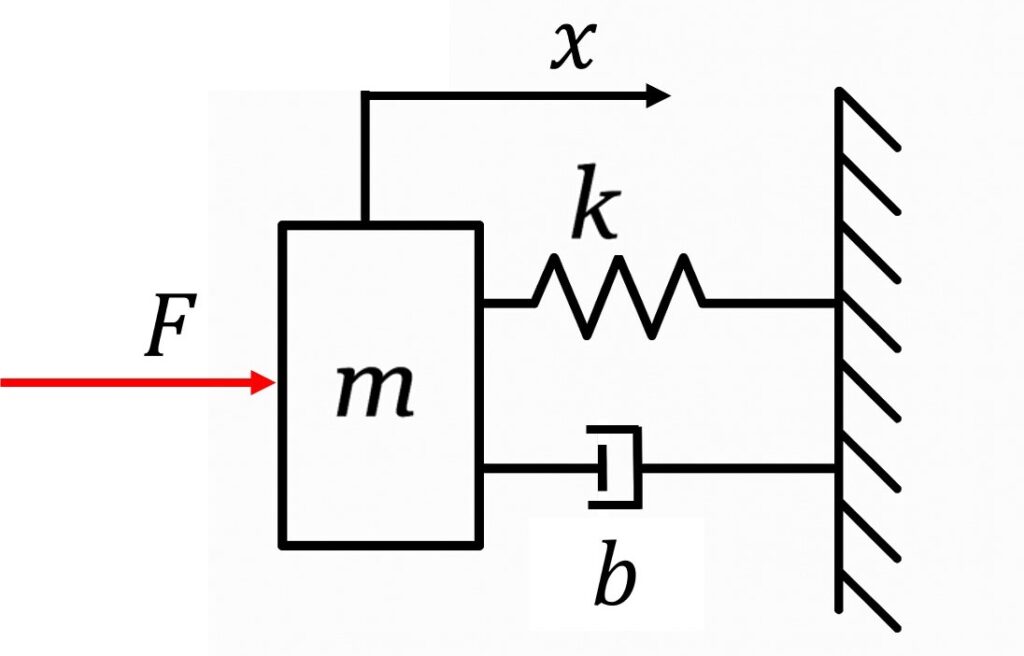
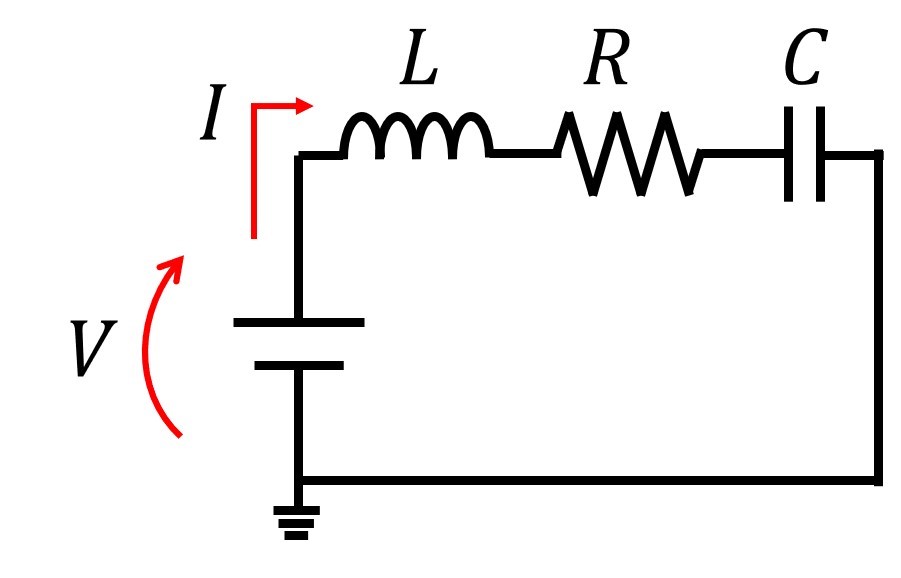
※図を見て、「電気回路ではRとCは直列だけど、力学のbとkは並列では?」と感じた方へ──
実はこの“並列と直列の違い”こそ、アナロジーの奥深さと限界を理解する鍵になります。
その疑問を深掘りする解説記事を、近日公開予定です。
➤【予定記事】バネ・ダンパの並列構成とRLC回路の本当の対応関係とは?
単位と意味から腑に落とす
さらに深く理解するために、それぞれの物理量の単位を比較してみましょう。
- 電圧 [V] = ジュール/クーロン → エネルギー / 電荷
- 力 [N] = ジュール/メートル → エネルギー / 距離
これは、電圧と力がどちらも「単位エネルギーあたりの影響力」を示す量であることを意味します。
また、インダクタンスLの単位 [H] = [V·s/A] は、「電流の変化に抵抗する慣性」のような性質を持ち、質量[m]に対応します。
キャパシタンスCの単位 [F] = [C/V] は、「電圧に対して電荷を蓄える能力」であり、バネ(k)の逆数に対応します。
こうした単位の比較を通じて、各要素がどんな物理的意味を持っているかを腑に落とすことができるのです。
キャパシタは“逆数”なのに、なぜバネに対応できるのか?
電気回路では、キャパシタ(コンデンサ)がバネに対応しています。
ところが、式を見るとキャパシタは「1/C」の形で現れ、バネの「F = kx」とは“逆数”の関係に見えてしまいます。
この違いに違和感を持つ方も多いのではないでしょうか。
この「逆数なのに対応する」という疑問を解消するには、数式の見た目ではなく、エネルギーのたまり方に注目するのがポイントです。
まず、バネは「変位 x に比例した力 F = kx を返す」装置です。
このとき、バネが蓄えるエネルギーは以下のように表されます:
E = (1/2) k x²
一方キャパシタは、「電荷 q をためると、電圧 V = q / C を返す」装置です。
エネルギーの式は以下のとおりです:
E = (1/2) q² / C または E = (1/2) C V²
つまり、どちらも「ためた量」に比例して「戻ろうとする出力」が出るという、同じ構造をしています。
ここで注目すべきは:
- バネは変形に比例して反力を返す装置
- キャパシタは電荷に比例して電圧を返す装置
つまり、どちらも「蓄えられた量(x や q)」に応じて「それを戻そうとする出力(F や V)」が出るシステムです。
- バネ定数 k が大きい → 少しの変位で大きな力 → “戻りたがり”が強い
- キャパシタンス C が大きい → 多くの電荷で少しの電圧 → “ためたがり”が強い
このようにみると、kとCが逆数の関係性にあることがイメージできるのではないでしょうか?
まとめ
本記事では、オームの法則を起点に、RLC回路と力学系との対応関係を整理してきました。
単に似ているというだけではなく、数学的にも同じ構造をしており、解析手法も共通です。
このようなアナロジーを活用すれば、目に見えない電気回路の挙動を、目に見える力学系としてイメージできるようになります。
そしてその視点は、流体・熱・音響など他の分野にも応用可能です。
他分野とのアナロジーについては、こちらの記事で詳しく解説しています。
物理法則のアナロジー一覧:F=maが示す多様な世界