目次
ニュートンの三法則
まずはおさらいとして、高校で習った基本法則を思い出してみましょう。
- 第1法則（慣性の法則）
→ 外から力が加わらなければ、物体は止まり続けるか、動き続ける。 - 第2法則（運動方程式）
→ 力を加えれば加速度が生まれる。これが F=ma。 - 第3法則（作用反作用の法則）
→ 力を加えれば、逆向きに同じ大きさの力が返ってくる。
（例：壁を押すと自分も押し返される感覚）
F=maはどこから来た？
- 昔は「力 ∝ 速度」と思われていたそうです。
摩擦や空気抵抗は目に見えず、周りに初めからあるんだから当然ですよね。 - ガリレオが「摩擦がなければ物体は等速直線運動」と発見。
- ニュートンがその上で「加速度こそが力の結果」と定義。
- 質量×加速度が力だとしたのが、F=ma という形。
F=maは証明できるのか？ ～実は「定義」だった話～
- 力とは何か？ を説明するために「質量×加速度」とした。
- つまり、「この式が成り立つように力を定義した」ということ。
- この式が物理学の始まり。これで世界を説明する枠組みができた。
- 単位（ニュートン）の基準もここから作られた。
→ 1N = 1kg・m/s² - でも、これまでの多くの実験がこの式の正しさを裏付けています。
→ 加速度 ∝ 力 / 質量 は、何度も確かめられてきた法則なのです。 - 光速に近い場合や、とても小さい量子の世界では、この式は成り立たないことからも経験則だということがわかるかと思います。
もっと詳しく知りたい人へ
- Javalab：F=maの基礎と図解
→ わかりやすいアニメーションでF=maの動きを確認できます。 - YouTube：ニュートンの法則を直感的に学べる動画（6:34）
→ アニメーションで法則を視覚的に理解できます。
現実のF=ma ～粘性・弾性を含めた運動方程式～
現実の運動は、摩擦やバネの力などが絡み合っています。
そのため、F=ma だけでは説明しきれない場面も多く、次のように拡張することがよくあります：
この式は、次の3つの力の和で成り立っています：
：質量による慣性力（F=ma部分） → ここで
（加速度）
：ダンパ（粘性）の抵抗力 → ここで
（速度）
：バネ（弾性）の復元力 → ここで
は変位
ここで「弾性」や「粘性」と難しく聞こえるかもしれませんが、
簡単にいえば、**位置や速度に比例して力を及ぼす“何か”**と捉えてもらえればOKです。
例えば、バネや空気抵抗がその代表例ですが、
実際のモノによっては**比例関係が成り立たない**場合もあります。
それでも、このシンプルな式に落とし込むことで、複雑な現象も計算や設計がしやすくなるため、多くの場面で活用されています。
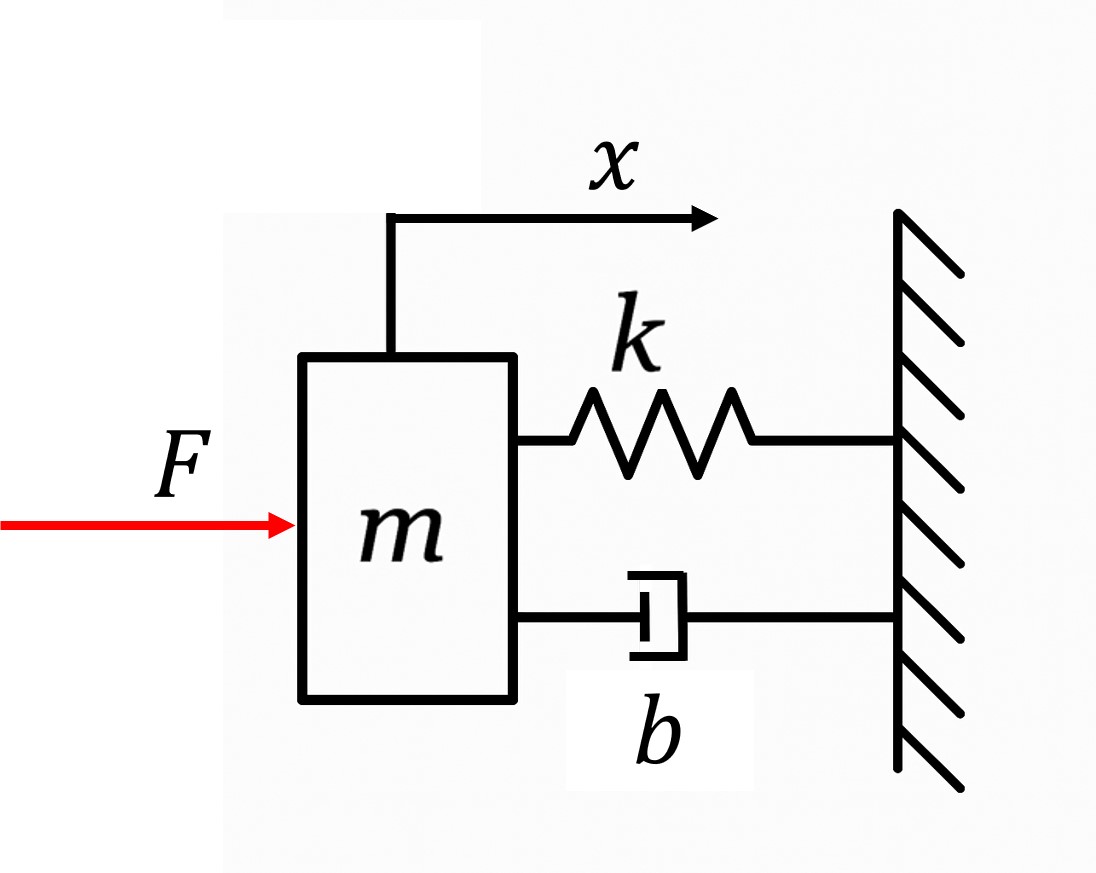
図でイメージ：
質量（m）、バネ（k）、ダンパ（c）が並んだ「バネマスダンパ系」
→ このモデルで現実の運動をシンプルに表せます。
※ プライム記号（ ‘ ）は時間微分を表します。
1回微分：速度、2回微分：加速度
まとめ
F=maは、運動の変化を力と質量の関係で捉える、物理の基本的な考え方です。
この構造は他の分野にも共通しており、回転運動や電気、流体、熱、音といった現象にも同じような対応関係が見られます。
コメント