ドアが一次遅れっぽい動きをしている
トイレから出るとき、ドアからパッと手を離したあの瞬間のことです。
ドアがオーバーシュートもせず、スーッと戻って「カチャン」と気持ちよく閉まりました。
そのとき、ふと思ったのです。
「この挙動、一次遅れ応答っぽいな……?」
ドアをモデル化してみる
このドアを物理モデルとして考えると、次のように表現できます。
パラメータ
- イナーシャ J:ドアの回転体としての慣性
- バネ k:ドア上部のくの字アームのねじりバネ成分
- ダンパ c:油圧や摩擦による粘性抵抗
- トルク入力 τ(t):手で一瞬押したときの外力トルク
運動方程式
回転系の運動方程式は以下のように書けます。
![]()
伝達関数
ラプラス変換すると、ドアの回転角と入力トルクの関係は:
伝達関数
![]()
一次遅れっぽいと思っていたのに、式を立ててみると しっかり2次遅れ系でした。
パラメータを見積もってみる
イナーシャJ
重さはおおよそ100kg、サイズは高さ2m・幅1mの直方体と見積もると、
![]()
長方形のイナーシャ(幅は無視)と並行軸の定理で見積もりました。
バネ定数k
1kgくらいの力で押した気がするので、入力トルクは
![]()
90度(=π/2 rad)ほど開けたのでねじりバネ定数は、
![]()
実際には非線形バネかもしれないけど、細かいことは気にしない。
ダンパ係数c
式は二次遅れでしたが、体感一次遅れに近かったので、
無理やり一次遅れ系に当てはめて、バネ項を無視して考えてみます。
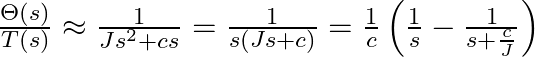
逆ラプラス変換すると
![]()
今回、手を放してから5秒くらいでしまったので、
以下の図から時定数は大体1秒として、
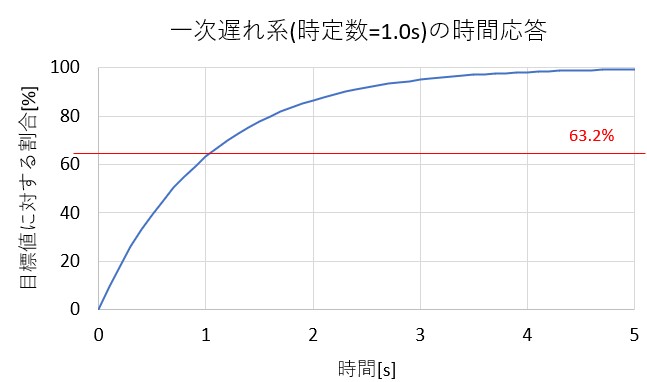
![]()
一般的な二次遅れ系との比較
一般に二次遅れ系は以下の式で表すことが多いです。
![]()
今回推定した値を当てはめてみると
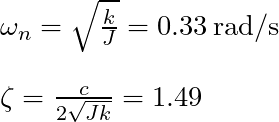
減衰係数 ζ > 1 のため過減衰系(オーバーシュートなく収束)であることがわかります。
一次遅れっぽいと感じたドアの動きは、実は過減衰の動きで説明ができそうです!
モデルと現実を比べてみる
ここまでの分析で、「このドアは過減衰な二次遅れ系だ」と見立てることができました。
ですが、本当にこのモデルで現実を再現できているのでしょうか?
それを確かめるには、モデルから得られる時系列応答を描いてみて、実機の動作と重ねてみることが重要です。
例えば、
実際にドアの開閉を動画撮影し、画像解析で角度変化をデータ化する。
推定したパラメータで二次遅れ系の応答をシミュレーションする。
両者を比較して、モデルの妥当性やズレの原因を考察する。
といった具合です。
この作業を通じて、次のステップへ進めます:
「cは本当に粘性抵抗だけで説明できるのか?」
「静摩擦や非線形バネ要素があるのでは?」
「ヒンジの構造的な遊びは?」
ここまでくれば、ただの「物理っぽい話」から一歩進んで、実用的なモデル化に近づけます。
もはや仕事ですね。
締め:日常と数式がつながる瞬間
今回は、ドアの動きを見て「一次遅れっぽいな」と思ったところから、
実際にモデルを立て、数式に落とし込むという流れをまとめました。
モデル化誤差の考察まではなかなかできませんが、ざっくりな推定でも、体感と理論が結びついた瞬間はとても心地よいものです。
書いているうちに、自分の理解の浅さに気づいたり、
「こういうことだったのか!」と再発見があったりして、いい復習にもなりました。
もしあなたも、「なんでこう動くんだろう?」と感じたことがあれば、
ぜひ一度モデル化してみてください。
物理と感覚がつながる瞬間、とても楽しいですよ。
以上、スムーズに閉まるドアを考えてみた話でした。

